【浦和周辺】塾で伸びない中学生専門の家庭教師、塚田です。

「時間内に解き終わらない」
「少し複雑な問題になると解けなくなる」
「証明や記述の問題が苦手」

そういった悩みを抱えている中学生のために、今回は「効率よく数学の北進テストで偏差値６５を取る方法」を解説します。

数学の北辰テストの配点は

という配点です。

偏差値65を取るためには、70点が目標点数となります。

・大問１で45点前後
・大問２、３で20点前後
・証明問題で7点前後

がそれぞれの目標点です。

基本問題と解きやすい標準レベルの問題をミスせずに解ければ、偏差値５５まではそこまで苦労せずにあげることができます。

基礎をしっかりと身につけた後は、学校では教わらない公式や、応用問題の楽な解き方を市販の参考書で身につけ、実践問題を繰り返し解きましょう。

大問1は簡単な問題が多い割に配点が高いです。

解けるかわからない問題に時間を使うよりも、まずは大問1で計算ミスをなくすように落ち着いて解きましょう。

大問2、3は中には難しい問題もありますが、標準レベルの実践問題を繰り返し解けば、７割は取れるようになります。

大門４の証明問題は嫌いな生徒も多く、証明分野は0点の生徒も多くいます。

証明問題で満点を取ることは確かに難しいですが、1問目の問題に正解することや、記述で部分点を稼ぐことは難しくありません。

出やすい証明問題を繰り返し解き、答案の書き方を身につけましょう。

読むだけでも点数が上がる！北辰テストで使える裏技

北辰テストで使える裏技①

通常の考え方であれば、

➀展開図を書く

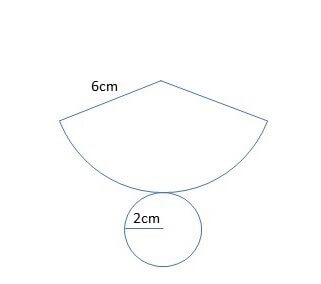
②半径６cmの円の円周を求める→１２πcm

③半径２ｃｍの円の円周を求める→４πcm

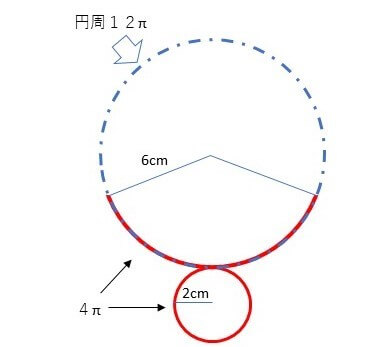
④１２π：６π ＝ 360°：Ｘ°で扇形の角度を出す

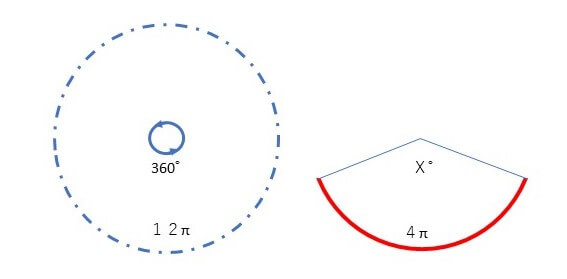
⑤半径６の円の面積（３６π）に１２０°/３６０°ををかけて扇形の面積を出す
⑥底面積（４π）と扇形の面積（１２π）を足す

というように解いていきます。

中一で習う問題ですが、求めるためには「数学的な考え方」と「多くの計算手順」が必要な問題となっています。

しかし、この問題。

実は、暗算で解けるのです。

その計算がこちらです。

半径と母線を足して、半径とπをかければ表面積は出せます。

北辰テストで使える裏技②

もうひとつ円錐に関する公式を紹介しておきます。

通常の解き方であれば、先ほどと同じように、

➀展開図を書く

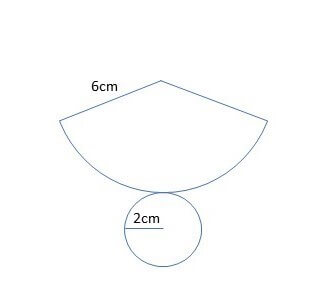
②半径６cmの円の円周を求める→１２πcm

③半径２ｃｍの円の円周を求める→４πcm

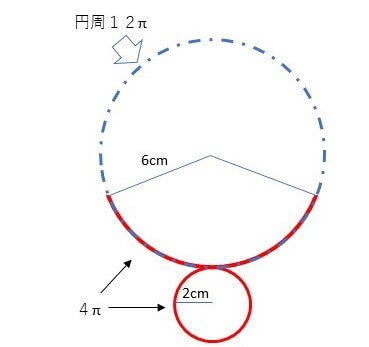
④１２π：６π ＝ 360°：Ｘ°で扇形の角度を出す

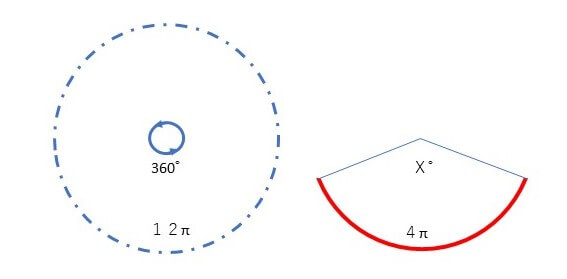
答え：X＝１２０°

こういった手順で解くことになりますが、
公式を使うと簡単に解くことができます。

この公式を知っていれば、

と一発で解くことができます。

北辰テストで使える裏技③

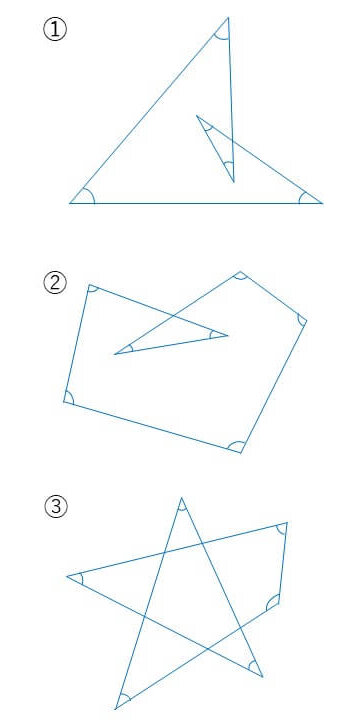
まずは通常の解き方です。

【問題①】

➀∠a＋∠b＝∠c＋∠d
であることを見つける

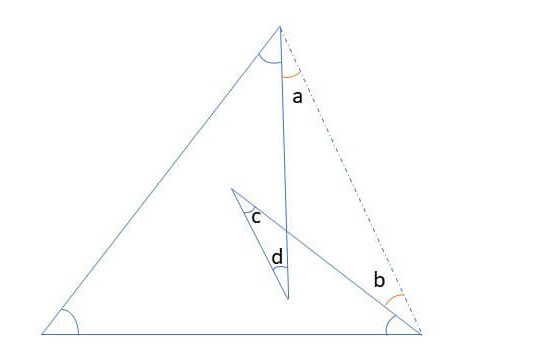
②三角形の和は180°であるので、
　答え180°

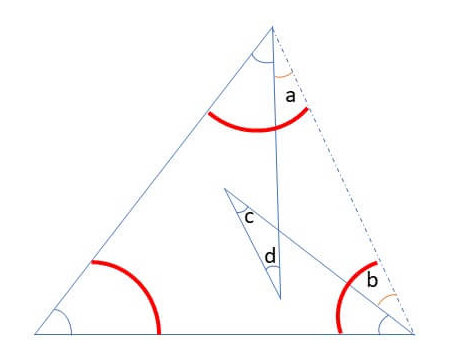
【問題②】

➀∠a＋∠b＋∠cが長方形のオレンジの線で示した角度と等しくなることを見つける

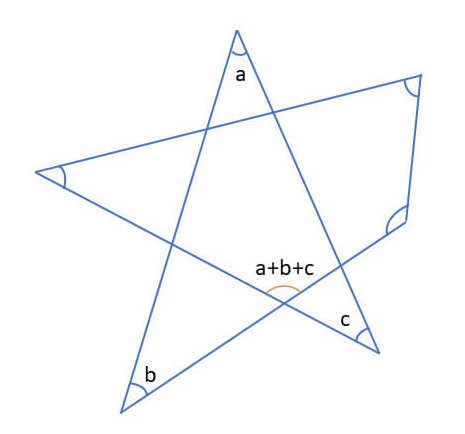
②四角形の内角の和は360°であることから、
　答え360°

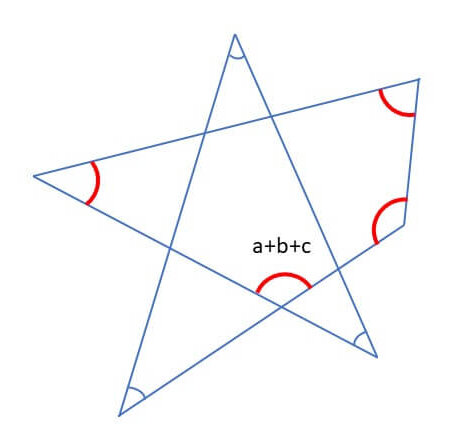
【問題③】

➀補助線を引く

②∠a＋∠b＝∠c＋∠dであることに気づく

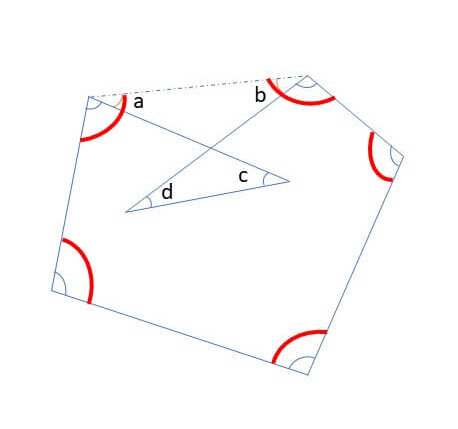
③五角形の内角の和は540°なので、
　答え540°

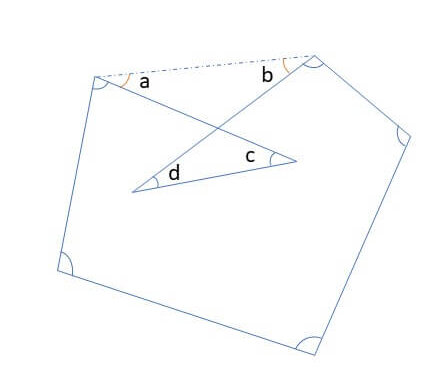
こういった角度が決まっていない問題を解くには、

➀角度の特殊な公式を覚える
②必要があれば補助線を引き、公式を使う
③「三角形」「四角形」「五角形」などの内角の和と同じであることを見つける

といった手順となります。

解説を見ると、答えまでに必要な過程と計算は少ないので、もしかしたら簡単な問題に見えるかもしれません。

しかし、実際に違う形の類題を解くとなると、角度が等しい箇所に気づけなかったり、気づくまでに案外時間がかかるものです。

この問題。裏技さえ知っていれば計算も気づく時間も必要ないです。

今回の裏技。それは、
「見た目で180°か360°か540°を判断する」
という方法です。

というのも、
こういった実際の角度を求める問題は

➀角度の特殊な公式を覚える
②補助線を引き、公式を使う
③「三角形」「四角形」「五角形」などの内角の和と同じであることを見つける

という手順で解くと説明しました。

つまり、最終的には「三角形」「四角形」「五角形」などの内角の和と同じであることを見つけることになるのです。

であれば、最初から答えは

・三角形の内角の和180°
・四角形の内角の和360°
・五角形の内角の和540°

のどれかになります。

（ちなみに、私立高校の過去問やレベルの高い問題集には720°や1080°が答えとなる場合もありますが、北辰テストや公立高校の問題では180°か360°か540°のどれかが答えになる問題しかみたことがありません。）

このことさえ知っていれば、数学の複雑な角度もの問題も得点することができるのです。

 

北辰テストで使える裏技④

この問題。文字で考えることにも慣れているが人であれば、
「もともとの牛乳の量を、一人当たりの牛乳の量で割ればいいんだな」
とわかるでしょう。

しかし、文字でおいてあるタイプの文章題が苦手な場合は、通常よりも難しく感じることでしょう。

実際、こういった問題の正答率は問題の難易度に比べて低い傾向があります。

では、この問題ではどうでしょうか？

この問題であれば、答えが２人だとすぐにわかるのではないでしょうか？

そう、文字で考えるとわからなくなってしまう問題でも、文字を具体的な数字にして考えれば解くことできるのです。

 先ほどの問題はどうして２人だとわかったかというと、
「５００mlを２人で飲むと、１０００mlだから」と答える人が多いです。

この
・「５００」
・「２」
・「１０００」
という数字を見れば、「１０００ｍｌ÷５００ｍｌ＝２人」という計算をしているのだとわかるでしょう。文章の文字と、仮に置いた数字を置き換えて、

と答えることができるのです。

もし、文章題でわからなくなった場合には、とにかく実際の数字を入れて考えてみましょう。

北辰テストで使える裏技⑤

この問題。通常であれば、

➀●と○をそれぞれ文字で置き換える。

②方程式を作る

2a＋2b＋ｘ°＝180°
ｘ°＝180°－2a－2ｂ
ｘ＝180°－２（a＋b）・・・①

a＋ｂ＋130°＝180°
a＋ｂ＝50°・・・②

③最後に作った方程式を解く

「ｘ＝180°－２（a＋b）」に「a＋ｂ＝50°」を代入すると、
ｘ＝180°－２×50°
ｘ＝80°

という求める方になります。

この問題を裏技を知っていれば、

教科書や参考書のように、わざわざ●と○を文字で置き換えたり、方程式を作る必要はありません。

どうやるかというと、
まず、●と○の角度を自分で決めてしまいます。

130°が含まれる三角形の和が180°になるように角度を当てはめましょう。
「１０°と４０°」や「１５°と３５°」など、組み合わせは何度でも大丈夫ですが、計算しやすい数字にしておくといいです。

今回は「３０°と２０°」で考えていきます。

●と○の角度はそれぞれ同じなので、残りも書き込みます。

書き込んだ角を足すと、次のようになります。

あとは、三角形の角度を全部足すと180°になるので、

180°－60°－40°＝100°
ｘは100°だと求めることができます。

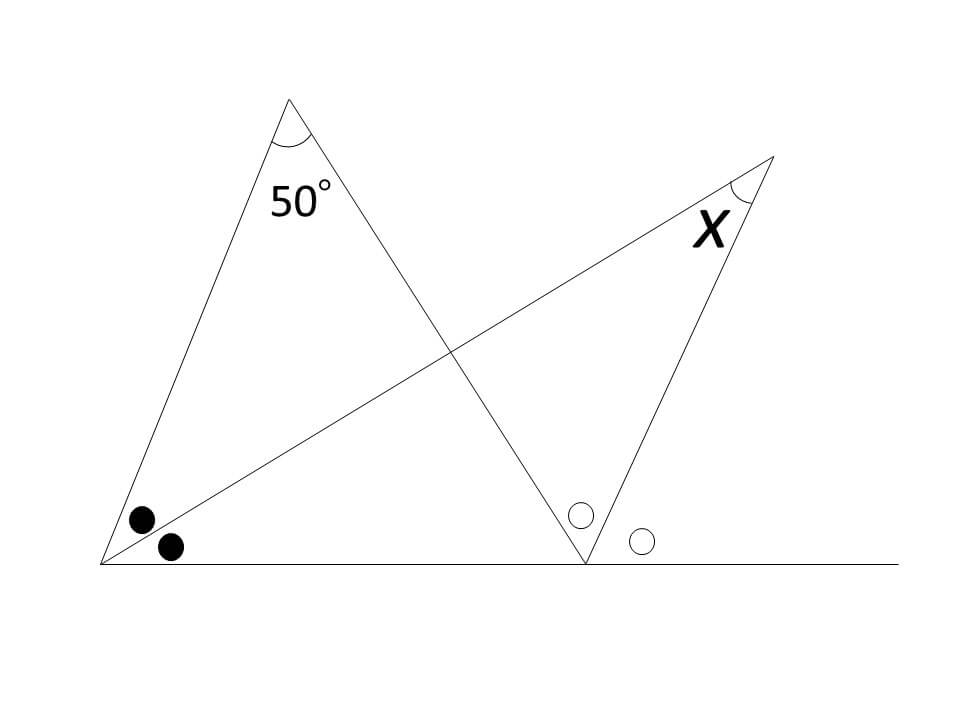
通常であれば、

➀●と○を文字に置き換える

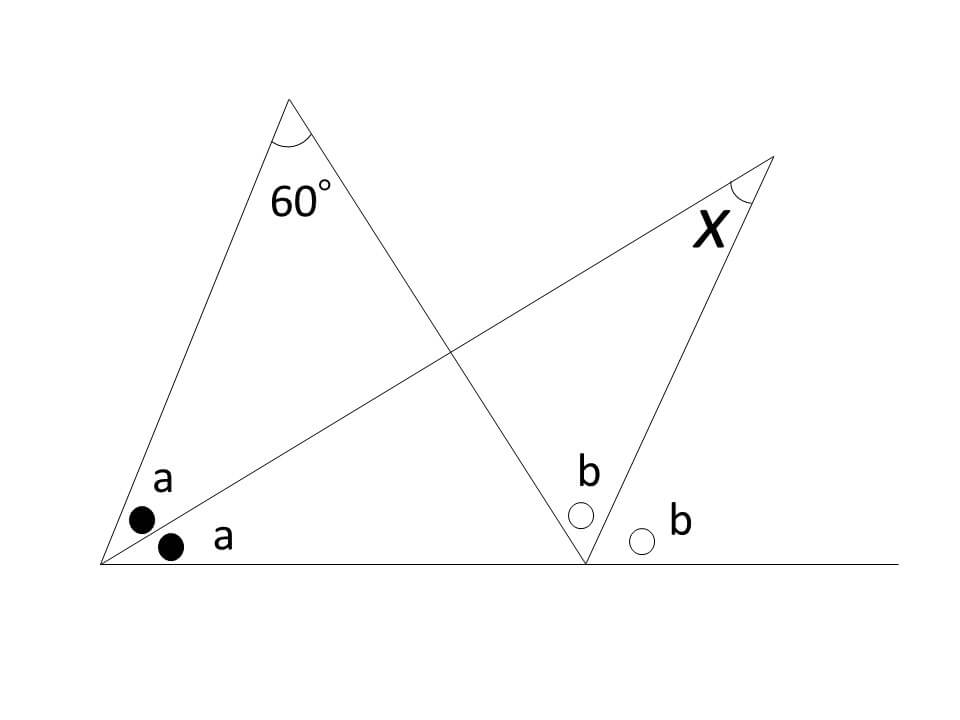
②外角の法則から2a＋60＝2bを作る

③外角の法則をもう一回使って、a＋ｘ＝b

2a＋60＝2b
→60＝2b－2a
→30＝b－a

a＋ｘ＝b
→ｘ＝b－a

よって、ｘ＝３０°

このような解き方となります。

この問題も先ほど説明した裏技を使って解くことができます。

裏技を使うと、数字を当てはめて

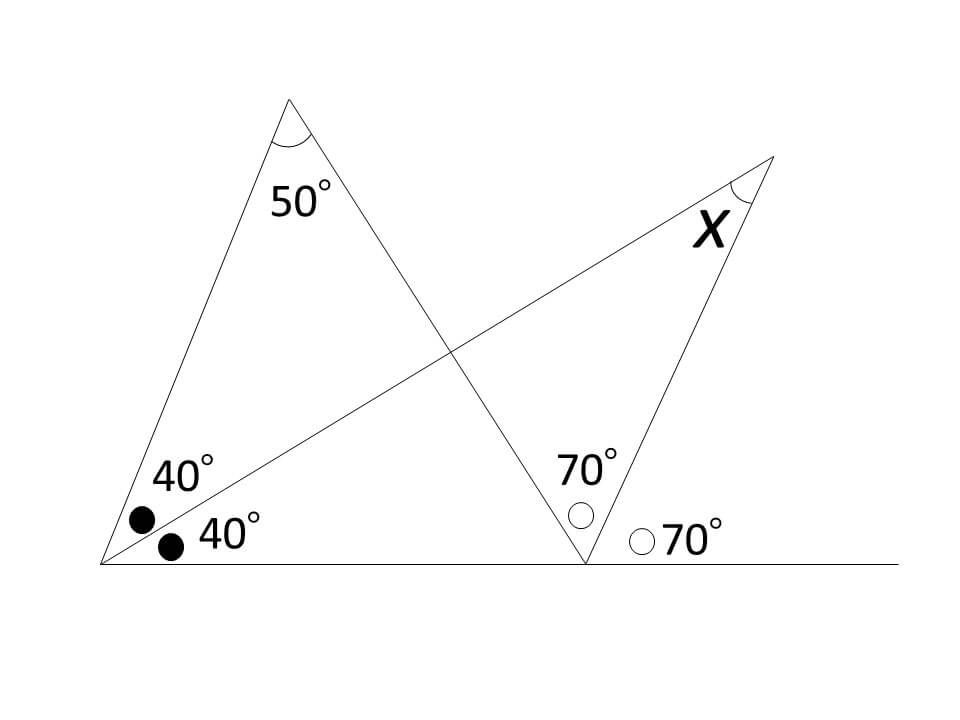
赤文字の箇所を出して、

180°－（40°＋40°＋70°）を計算し、

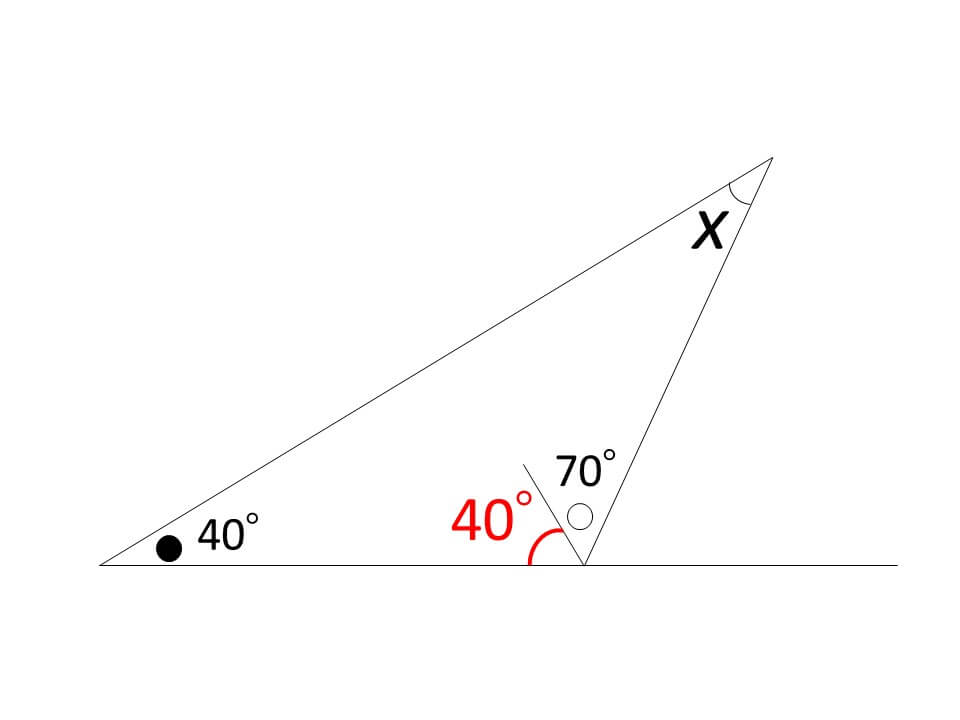
X＝３０°が答えとなります。

北辰テストの偏差値ごとのオススメ参考書

偏差値～５０

「中(１・２・３)数学をひとつひとつわかりやすく。」

図が大きく書いてあり、解説がわかりやすいのが特徴です。

まずは基礎の部分をしっかりと理解できるようにしましょう。
授業の予習をする際にもオススメの参考書です。

偏差値５０→５５

「入試に向けてまとめるノート　中学数学　」


この問題集は、基礎～標準レベルの入試問題を実際のノートに書くように、計算の過程や、つまづきやすいポイントが書いてあります。

過程がしっかりと書いてあるので、1人でも勉強しやすいつくりになっています。

偏差値５５→６５

「塾で教える高校入試 数学 塾技100」（各ページの入試問題をチェックの箇所まで）

この参考書の特徴は、進学塾で実際に教えてる学校では教わらない公式や、計算を楽にする裏ワザをたくさん書いていることです。

数学は短い時間で解くこと、ミスを減らすことが入試においてはすごく重要になります。

この公式や裏ワザを知っているだけで、難しい問題を楽に解けるようになったり、複雑な計算をしなくても答えを出せるようになります。

この参考書通りの効率のいい解き方を身につければ、成績は一気に上がり、数学を得意科目にすることができるでしょう。

「中学数学 図形の証明がらくらく解ける。」

証明の基本問題が穴埋め形式と記述形式の2つが載っています。
穴埋めだけでなく、記述の問題も繰り返し解き、減点されない回答を作れるようにしましょう。

番外編　６５→７０

・「塾で教える高校入試 数学 塾技100」(別冊解答の問題まで全部)

応用問題や難関私立の入試問題が、載っています。公式や裏ワザを使い、ミスなく答えを出せるようにして下さい。


・「数学証明のコツ ―入試必出の証明問題の解き方がわかる!!」

応用問題や私立の入試問題の良問が多く載っています。証明の応用問題も、基本パターンの組み合わせでできていますので、良問を繰り返し解くことで、解き方のパターンが身につき、正解できるようになります。

まとめ

•大問1の基礎問題は、簡単な割に配点が高いので、ミスしないことが重要

•証明問題は比較的難しくない、1問目の問題と記述の部分点を稼ぐ

•基本問題が解けるようになった後は塾技100を使い、解き方のテクニックや学校で習わない公式を覚える